Blog Magnetico

 UNIDAD 4. CAMPO MAGNÉTICO.

4.1 CONCEPTOS: MAGNETISMO, CAMPO MAGNÉTICO Y FLUJO MAGNÉTICO.

MAGNETISMO. 

Se le denomina así a un fenómeno físico por el que los materiales ejercen fuerzas de atracción o repulsión sobre otros materiales. Estos presentan un polo positivo y otro negativo caracterizado por fuerzas dipolo. La propiedad dipolo magnética establece que los polos iguales se repelen y los polos opuestos se atraen.

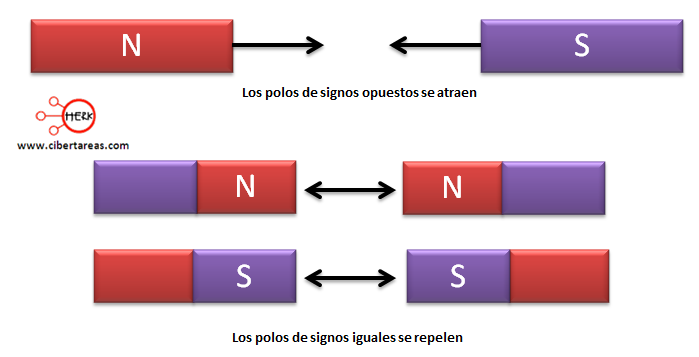
Para que se produzca el magnetismo deben existir cargas en movimiento como por ejemplo los electrones, siendo estos los responsables de la capacidad magnética de un material u otro. 

El electrón es una partícula que forma parte de la estructura atómica y funciona como un pequeño imán. y en un imán los electrones tienden a orientarse en la misma dirección creando una fuerza magnética grande o pequeña dependiendo del número de electrones que estén orientados. Así, un cuerpo con electrones orientados en una dirección X se atraerá a otro orientado a una dirección Y, generando un campo magnético entre ambos.

CAMPO MAGNÉTICO. 

Se trata de un campo que ejerce fuerzas (denominadas magnéticas) sobre los materiales en otras palabras es un sector del espacio el cual es invisible el cual ejerce fuerzas magnéticas sobre sustancias o materiales sensibles al magnetismo. En términos matemáticos es la cantidad de fuerza ejercida en una carga en movimiento. La carga, la velocidad y el campo magnético se relacionan con el resultado del vector.

Representación visual de campo magnético.

Puede generarse por la cercanía de un imán con una corriente eléctrica o con un campo eléctrico cambiante.

El campo magnético también es un campo vectorial como lo es el campo eléctrico pero a diferencia de este, el campo magnético no produce ningún efecto sobre cargas en reposo. Sin embargo, el campo magnético tiene influencia sobre cargas eléctricas en movimiento.

Si una carga en movimiento atraviesa un campo magnético, la misma sufre la acción de una fuerza (denominada fuerza magnética). Esta fuerza no modifica el módulo de la velocidad pero sí la trayectoria.

El campo magnético se denomina con la letra B y en el Sistema Internacional de Unidades se mide en tesla. Un tesla es el valor de un campo magnético que provoca una fuerza de un newton sobre una carga de un coulomb que se mueve perpendicularmente a éste, a una velocidad de 1 m/s.

El campo magnético generado por una única carga en movimiento se calcula a partir de la siguiente expresión:

• Si q es positiva, el sentido de es es el de ; si q es negativa, el sentido es el contrario.
•  = 0 en todos los puntos de la dirección de .
•  Las lineas de campo son circunferencias concéntricas situadas en planos perpendiculares a .

El sentido del campo magnético viene dado por la regla de la mano derecha:

FLUJO MAGNÉTICO.

El flujo magnético Φ es la cantidad de líneas de fuerza que salen por un polo y que pasan a través de un área determinada en el espacio. 

Se calcula a partir del campo magnético, la superficie sobre la cual actúa y el ángulo de incidencia formado entre las líneas de campo magnético y los diferentes elementos de dicha superficie. La unidad de flujo magnético en el Sistema Internacional de Unidades es el weber y se designa por Wb.
En el sistema cegesimal se utiliza el maxwell (1 weber =108 maxwells).

La formula para calcular el flujo magnético es la siguiente:

Las tres formas que hay de variar con el tiempo el flujo de un campo magnético a través de una superficie: 

• Cuando el campo cambia con el tiempo B(t).
• Cuando el área de la espira cambia con el tiempo A(t).
• Cuando el ángulo entre el vector campo B y el vector superficie A cambia con el tiempo q(t). 

En el caso de que la Inducción magnética sea uniforme, podemos usar la expresión:

Donde: Φ es el flujo magnético

B es el vector inducción magnética

S es el vector superficie, que por convenio es normal a la superficie

θ es el ángulo que forman B y S

4.2 MATERIALES MAGNÉTICOS Y SUS PROPIEDADES. HISTERESIS.

En los materiales magnéticos se observa que sus átomos o iones se comportan como si fuesen pequeños imanes que interactúan entre si.Se dice que los átomos tienen un momento magnético diferente de cero, se caracteriza por su magnitud y la dirección en la que esta orientada. 

 Existen unos cuantos materiales que son magnéticos de forma natural o que tienen el potencial para poder convertirse en imanes como lo son: 

• Hierro
• Hematita
• Magnetita
• Gases ionizados

Existen dos tipos de materiales: materiales magnéticos blandos y magnéticos duros. 

• Los blandos se utilizan en aplicaciones en las cuales el material debe imanarse y desimanarse fácilmente, como en núcleos de transformadores para la distribución de energía eléctrica y como materiales para estatores y rotores de motores y generadores.
• Los materiales magnéticos duros se utilizan para aplicaciones que requieran imanes que no se desimanen fácilmente, como en los imanes permanentes de los altavoces, receptores telefónicos, motores síncronos sin escobillas y motores de arranque para automóviles.

PROPIEDADES MAGNÉTICAS. 

Cada material reacciona distinto a un campo externo, por lo que se clasifican entres tipos: 

MATERIALES DIAMAGNÉTICOS. 

 Esta propiedad existe entre átomos que poseen una estructura electrónica simétrica y no poseen momentos magnéticos producidos  por otro átomo permanente, estos forman enlaces iónicos. 

Al aplicar un momento magnético externo estos materiales se magnetizan muy levemente. Un imán repele levemente estos  materiales y estos no recuperan sus característica  al quitar el campo externo.

Ejemplos:

Grafito (diamagnetismo especialmente alto), cobre de plata, oro, plomo, bismuto, cinc, cadmio, mercurio, estaño, geranio, antimonio y arsénico.

Demostración visual de como el grafito ejerce repulsión sobre un campo magnético.

MATERIALES PARAMAGNÉTICOS.

 Existe en átomos que poseen una estructura electrónica no equilibrada y por lo tanto poseen un momento magnético propio, aunque débil.

Al aplicar un campo magnético externo el campo propio tiende a tomar la misma dirección y sentido del campo externo: magnetización débil. Un imán atrae levemente a estos materiales.

  

Ejemplos:

Litio, Aluminio, Magnesio, Cromo, Vanadio, Titanio, Molibdeno, Renio, Wolframio.

MATERIALES FERROMAGNÉTICOS

Poseen capas "d" incompletas y ademas tienen alineados su spin con los átomos adyacentes, sin un campo externo aplicado; esto ocurre en un volumen de cierta magnitud llamada "dominio".

Presentan un momento magnético propio relativamente fuerte en ausencia de un campo externo.

Ejemplos: Hierro, Cobalto, Níquel y Gadolino. 

  

HISTÉRESIS MAGNÉTICA

Es el fenómeno que ocurre cuando un material ferromagnético, sobre el cual ha estado actuando un campo magnético, cesa la aplicación de éste, el material no anula completamente su magnetismo, sino que permanece un cierto magnetismo residual. Esto  permite el almacenamiento de información en los imanes de los discos duros o flexibles de los ordenadores: el campo induce una magnetización en el pequeño imán, que se codifica como un 0 o un 1. Esta codificación permanece en ausencia de campo, y puede ser leída posteriormente, pero también puede ser invertida aplicando un campo en sentido contrario. 

LA CURVA DE HISTÉRESIS 
Muestra la curva de magnetización de un material. Sea cual sea el material específico, la forma tiene características similares.

• Al principio, la magnetización requiere un mayor esfuerzo eléctrico. Este intervalo es la llamada zona reversible.
• En un determinado punto, la magnetización se produce de forma proporcional. En ese punto se inicia la denominada zona lineal.
• Finalmente, se llega un instante a partir del cual, por mucha fuerza magnética que induzcamos al material, ya no se magnetiza más. Este es el llamado punto de inducción de saturación, que determina el inicio de la llamada zona de saturación. 

 

Ciclo de histéresis.

CICLO DE HISTÉRESIS (también lazo o bucle de histéresis) de un determinado material magnético.Se supone que una bobina crea sobre dicho material magnético una intensidad de campo H, el cual induce en ese material magnético una inducción (valga la redundancia) de valor B.
Así a un intensidad de campo H0 le corresponderá una inducción de valor B0.
Si ahora aumenta H (aumentando la corriente que circula por la bobina) hasta un valor H1, B también aumentará hasta B1. 

 Pero si ahora si restituimos H a su valor inicial H0 , B no vuelve a B0 , sino que toma un valor diferente B2. (Observe que el camino "a la ida" es distinto que "a la vuelta" lo que implica que para restituir la inducción en el núcleo a su primitivo valor, es preciso aplicar una corriente suplementaria de signo opuesto).

 Cada material tiene su propio lazo de histéresis característico.

 INSTRUMENTO DE MEDICIÓN DEL CICLO DE HISTÉRESIS

Se puede utilizar el magnetómetro de KÖPSEL que se encarga de proporcionar al material ferromagnético para modificar el sentido de los imanes.

4.3 Generación de campos magnéticos. Ley de Biot-Savart

Se cree que existen dos ingredientes fundamentales en la generación de un campo magnético. Estos dos ingredientes son:

• material magnético
• corrientes en movimiento dentro del material magnético.

 CAMPO MAGNÉTICO CREADO POR UNA CORRIENTE ELÉCTRICA CUALQUIERA.

Jean Biot y Savart establecieron después de que Oersted divulgara que al igual que una carga origina un campo eléctrico o una masa un campo gravitatorio, un elemento de corriente genera un campo magnético. Un elemento de corriente es la intensidad que fluye por una porción tangente al hilo conductor de longitud infinitesimal y cuyo sentido es el de la corriente eléctrica.

La ley de Biot y Savart establece que el campo magnético producido por una corriente cualquiera en un punto P viene determinado por la siguiente expresión:

 

Campo magnético creado por una corriente eléctrica rectilínea

 El valor del campo magnético creado por una corriente rectilínea en un punto P se obtiene por medio de la siguiente expresión:

 

 Las líneas de campo creadas por este tipo de corriente son circunferencias concéntricas al conductor y perpendiculares a él. Esto implica que la dirección del campo magnético sea tangente a ellas en cada punto y su sentido venga dado por la regla de la mano derecha. La regla de la mano derecha determina que si usamos el pulgar de dicha mano para indicar el sentido de la intensidad de corriente, el resto de dedos nos indicará el sentido del campo magnético.

 

Campo magnético creado por una corriente eléctrica que circula por una espira

 El valor del campo magnético en el centro de una espira circular creado por una corriente eléctrica se obtiene por medio de la siguiente expresión:

 

 Las líneas de campo creadas por este tipo de corriente son circunferencias concéntricas en cada punto del conductor, de tal forma que en el centro de la espira el campo magnético es perpendicular a la espira y el sentido se obtiene aplicando la regla de la mano derecha.

 

 

 

 

4.4 FUERZA MAGNÉTICA SOBRE UNA CARGA 

 Sobre una carga eléctrica en movimiento que atraviese un campo magnético aparece una fuerza denominada fuerza magnética. Ésta modifica la dirección de la velocidad, sin modificar su módulo.

 

 

 Fm = Fuerza magnética [N]
q = Valor de la carga [C]
v = Velocidad [m/s]
B = Campo magnético [T]
θ = Ángulo [grados o radianes]

El sentido se calcula por la regla de la mano derecha (índice = velocidad, mayor = campo, pulgar = fuerza, formando 90 grados entre cada uno de los tres dedos).

El sentido de la fuerza es para cargas positivas. Si las cargas son negativas el sentido es el opuesto al obtenido con la regla de la mano derecha.

4.5 FUERZA MAGNÉTICA SOBRE UN CONDUCTOR QUE CONDUCE CORRIENTE.

Una corriente eléctrica es un conjunto de cargas en movimiento. Conocida ya la fuerza que el campo B ejerce sobre una única carga, calculamos ahora la fuerza sobre un conductor por el que circula una corriente.

Fuerza sobre un conductor rectilíneo

Imaginemos un conductor rectilíneo de sección A por el que circula una corriente eléctrica I. La fuerza a la que se ve sometido cuando se encuentra en un campo B uniforme será la suma de la fuerza sobre todas las cargas.

Si n es el número de cargas q por unidad de volumen, y v_d la velocidad de desplazamiento de las mismas, el número de cargas en un elemento de volumen de longitud l es:

 

por lo que la fuerza total se calculará multiplicando el número de cargas por la fuerza ejercida sobre cada una de ellas:
 

Fuerza sobre un conductor de forma arbitraria

Si el conductor tiene sección constante pero una forma arbitraria y el campo no es uniforme, la fuerza se calcula mediante la integral, tomando un elemento diferencial de corriente según el sentido de la intensidad:

 

Aunque el conductor no sea rectilíneo, si el campo B es uniforme la expresión anterior se simplifica ya que se puede sacar B fuera de la integral. Entonces, según se aprecia en el dibujo, la fuerza total que B ejerce sobre el conductor de longitud l no rectilíneo es la misma que ejercería en caso de que el conductor fuera rectilíneo y uniera los puntos inicial (a) y final (b) del conductor (l´)

 

4.6 FUERZAS MAGNÉTICAS ENTRE DOS CONDUCTORES 

Hasta ahora has visto el campo magnético producido por una corriente en un conductor, pero ¿qué ocurre si existe más de un circuito? Ampère descubrió que dos corrientes eléctricas circulando en paralelo podían repelerse o atraerse con fuerzas magnéticas directamente proporcionales a las intensidades de cada una de ellas. Esto es fácilmente demostrable a partir de la ley de Biot y Savart

Si se tienen dos conductores rectilíneos paralelos por los que circulan dos corrientes eléctricas del mismo sentido I₁ e I₂. Tal y como muestra la figura ambos conductores generarán un campo magnético uno sobre el otro, dando lugar a una fuerza entre ellos.

Para calcular el valor de dicha fuerza en primer lugar se obtiene, según la ley de Biot y Savart, el campo magnético producido por el conductor 1 sobre el 2, que vendrá dado por la ecuación: 

Este campo magnético, ejerce sobre un segmento L del conductor 2 por el que circula una corriente de intensidad I₂, una fuerza cuyo módulo será el ya calculado en el apartado 2.3 para conductores rectilíneos: 

Dado que, tal y como se observa en la imagen, el campo magnético es perpendicular al conductor, el ángulo formado en este caso será de 90°, y sustituyendo el valor antes calculado  que para el campo 

se obtiene:

 

Si ahora calculáramos la fuerza que ejerce el conductor 2 sobre el conductor 1 llegaríamos exactamente al mismo valor:

 

Por tanto ambas fuerzas son del mismo módulo y dirección, están contenidas en el mismo plano y su dirección es perpendicular a ambos (observa la imagen). El sentido depende de la dirección de la corriente, si ambas tienen el mismo sentido su producto será siempre positivo y apuntarán de un cable hacia el otro atraiéndolos, mientras que si tienen sentidos contrarios, el producto será negativo y se dirigirán hacia afuera, tendiendo a separar los conductores

Nota:

La fuerza magnética ejercida entre dos conductores rectilíneos por los que circula una corriente eléctrica está contenida en el plano que forman ambos conductores y es perpendicular a los mismos, siendo el valor de su módulo:  

Esta fuerza es atractiva cuando las corrientes tienen el mismo sentido y repulsiva si el sentido es opuesto

4.7 LEY DE FARADAY

Es la fuerza electromotriz inducida en un circuito es igual y de signo opuesto a la rapidez con que varia el flujo magnético que atraviesa un circuito, por unidad de tiempo.

Relaciona la razón de cambio de flujo magnético que pasa a través de una espira o lazo con la magnitud de fuerza electromotriz inducida en la espira.

 

 

 La ley de Faraday es una relación fundamental basada en las ecuaciones de Maxwell. Sirve como un sumario abreviado de las formas en que se puede generar un voltaje (o fem), por medio del cambio del entorno magnético. La fem inducida en una bobina es igual al negativo de la tasa de cambio del flujo magnético multiplicado por el número de vueltas (espiras) de la bobina. Implica la interacción de la carga con el campo magnético. 

 4.8 LEY DE LENZ

Es una consecuencia del principio de conservación de la energía aplicado a la inducción electromagnética. Fue formulada por Heinrich Lenz en 1833. Mientras que la ley de Faraday nos dice la magnitud de la FEM producida, la ley de Lenz nos dice en qué dirección fluye la corriente, y establece que la dirección siempre es tal que se opone al cambio de flujo que la produce. Esto significa que cada campo magnético generado por una corriente inducida va en la dirección opuesta al cambio en el campo original.

Incorporamos la ley de Lenz a la ley de Faraday con un signo menos, que nos permite utilizar el mismo sistema de coordenadas para el flujo y la FEM. A veces nos referimos al resultado como la ley de Faraday-Lenz,

 

Frecuentemente lidiamos con la inducción magnética en espiras múltiples de alambre, donde cada una contribuye con la misma FEM. Por esta razón, incluimos un término adicional $N$ para representar el número de vueltas, es decir,

 4.9 INTRODUCCIÓN A LAS LEYES DE MAXWELL

Las ecuaciones de Maxwell permitieron ver en forma clara que la electricidad y el magnetismo son dos manifestaciones de un mismo fenómeno físico, el electromagnetismo.

 La diferencia más importante es que la magnitud y la dirección de la fuerza electromagnética dependen de la carga del cuerpo que lo produce y también de su velocidad.

 Maxwell inventó un concepto que se ha utilizado constantemente en la física: el campo electromagnético. Según esta interpretación, en todo punto del espacio alrededor de una carga existe una fuerza electromagnética, cuya intensidad y dirección están definidas por medio de unas fórmulas matemáticas. En realidad, más que un concepto, el campo es una definición que da cierta consistencia a la idea de que una carga eléctrica actúa sobre otra lejana, sin tener que recurrir a una acción a distancia.

Las ecuaciones de Maxwell surgen a partir del electromagnetismo y son el resumen de esta teoría desde un punto de vista macroscópico.

 Son la descripción del campo electromagnético: el campo eléctrico, el campo magnético, su origen, comportamiento y relación entre ellos, incluyendo las ondas electromagnéticas como la luz. Básicamente, con estas ecuaciones es posible saber cómo va ser y cómo va a comportarse el campo electromagnético en una región determinada, a partir de las cosas que hay allí. La contrapartida, es decir, qué le pasa a las cosas que hay allí a partir del campo electromagnético, está descrita por la fuerza de Lorentz, de la que no vamos a hablar hoy. El conjunto de estas ecuaciones describe cosas como la corriente eléctrica, los imanes, los rayos, la electricidad estática, la luz, las microondas, la radio, etc.

 Elaboro: 

• Pérez Navarro Isai
• Sérvin Pérez Paola Sarahí

REFERENCIAS BIBLIOGRÁFICAS

• Anónimo. (Sin Fecha). Qué es Magnetismo. Noviembre 24, 2018, de Significados Sitio web: https://www.significados.com/magnetismo/
• Pino, F. (2010). Qué es el magnetismo. Noviembre 24, 2018, de VIX Sitio web: https://www.vix.com/es/btg/curiosidades/2010/07/31/que-es-el-magnetismo
• González, P. (Sin Fecha). ¿Qué es un campo magnético?. Noviembre 24, 2018, de VIX Sitio web: https://www.vix.com/es/ciencia/172863/que-es-un-campo-magnetico
•  Anónimo . (Sin fecha). Diamagnetismo. Noviembre 25, 2018, de ecured Sitio web: https://www.ecured.cu/Diamagnetismo
•  Fernandez J & Coronado G. (Sin fecha). Ley de biot-Savart. Noviembre 24, 2018, de Fisicalab Sitio web: https://www.fisicalab.com/apartado/campo-magnetico-creado-corriente-electrica#contenidos
• Blas, T & Serrano, A. (Sin Fecha). Campo Magnético. Noviembre 26, 2018, de UPM Sitio web: http://www2.montes.upm.es/dptos/digfa/cfisica/magnet/fuerzamag2.html
• Anónimo. (Sin Fecha). 4. Fuerzas entre corrientes paralelas. Definición de Amperio. Noviembre 26, 2018, de catedu Sitio web: http://e-ducativa.catedu.es/44700165/aula/archivos/repositorio/3000/3232/html/4_fuerzas_entre_corrientes_paralelas_definicin_de_amperio.html
•  Gomez, P. (2011). Las ecuaciones de Maxwell. Noviembre 25, 2018, de El tamiz Sitio web: https://eltamiz.com/2011/08/10/las-ecuaciones-de-maxwell-introduccion-historica/